Breaking Caesar cipher

Intro

Let’s say you found somewhere on the web message similar to this:

Hey buddy, do you want to work at Acme Corporation? We’re waiting for you! Here’s instruction how to submit your CV: 132 161 181 93 92 143 161 161 169 175 92 168 165 167 161 92 181 171 177 92 175 171 168 178 161 160 92 171 177 174 92 159 164 157 168 168 161 170 163 161 93 92 147 161 92 170 161 161 160 92 172 161 171 172 168 161 92 168 165 167 161 92 181 171 177 93 92 140 168 161 157 175 161 92 175 161 170 160 92 181 171 177 174 92 175 171 168 177 176 165 171 170 92 157 170 160 92 127 146 92 176 171 92 165 159 157 170 158 174 161 157 167 159 165 172 164 161 174 175 124 157 159 169 161 106 159 171 169 92 173 177 171 176 165 170 163 92 174 161 162 161 174 161 170 159 161 118 92 171 133 129 164 158 169 133 181 150 147 130 161 149 110 168 165 179 137 128 181 159 179 106

Most likely those numbers are encoded ASCII and chances are this text is encoded using Caesar cipher.

In order to break it you can, first of all, read mentioned wiki link, that introduces several approaches, or you can read further to see how to do it using python and matplotlib (everyone likes charts, right?).

Analysis

We assume that encrypted message contains regular text phrase with spaces and it’s written in English (or any other language that you can understand or have a way to check if some sequence of characters is a valid word in a target language)

Source text

In order to understand how to read an encrypted text, let’s have a look at a frequency distribution polar bar plot of an unencrypted text. For example:

There is no one who loves pain itself, who seeks after it and wants to have it, simply because it is pain.

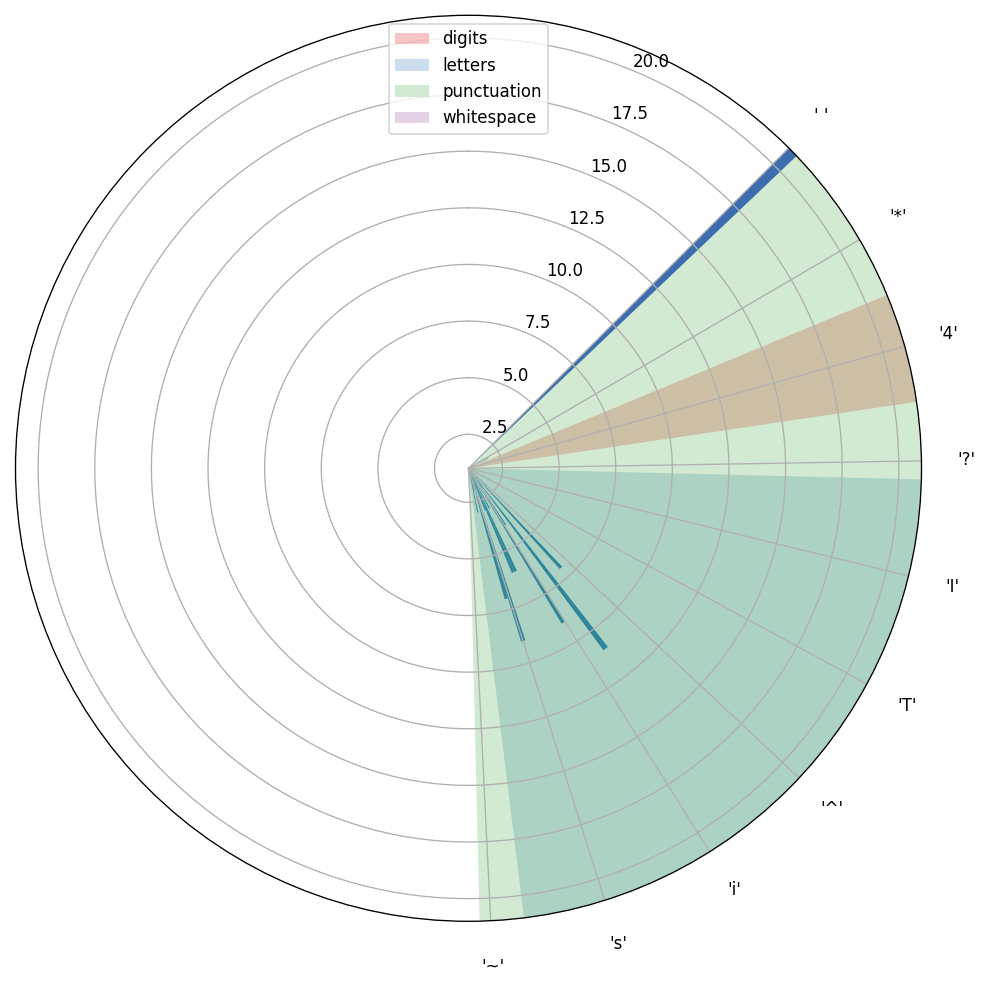
As you can see space is the most frequent character in this sentence. Vast majority of other characters fall into lowercase letters section.

More importantly, this sequence has boundaries, which are defined by all printable characters. It starts at 32 (‘ ‘) and ends at 126 (‘~’). The phrase itself (its character distribution to be precise), also has boundaries. It starts at 32 (‘ ‘) and end at 121 (‘y’). Keep this in mind as it might be useful later.

Encrypted text

Let’s now apply simple Caesar cipher with 150 as a shift to the text and have a look at the distribution plot again, but this time for an encrypted sequence.

Here’s what the sequence looks like after the encryption:

234 254 251 8 251 182 255 9 182 4 5 182 5 4 251 182 13 254 5 182 2 5 12 251 9 182 6 247 255 4 182 255 10 9 251 2 252 194 182 13 254 5 182 9 251 251 1 9 182 247 252 10 251 8 182 255 10 182 247 4 250 182 13 247 4 10 9 182 10 5 182 254 247 12 251 182 255 10 194 182 9 255 3 6 2 15 182 248 251 249 247 11 9 251 182 255 10 182 255 9 182 6 247 255 4 196

And a corresponding graph:

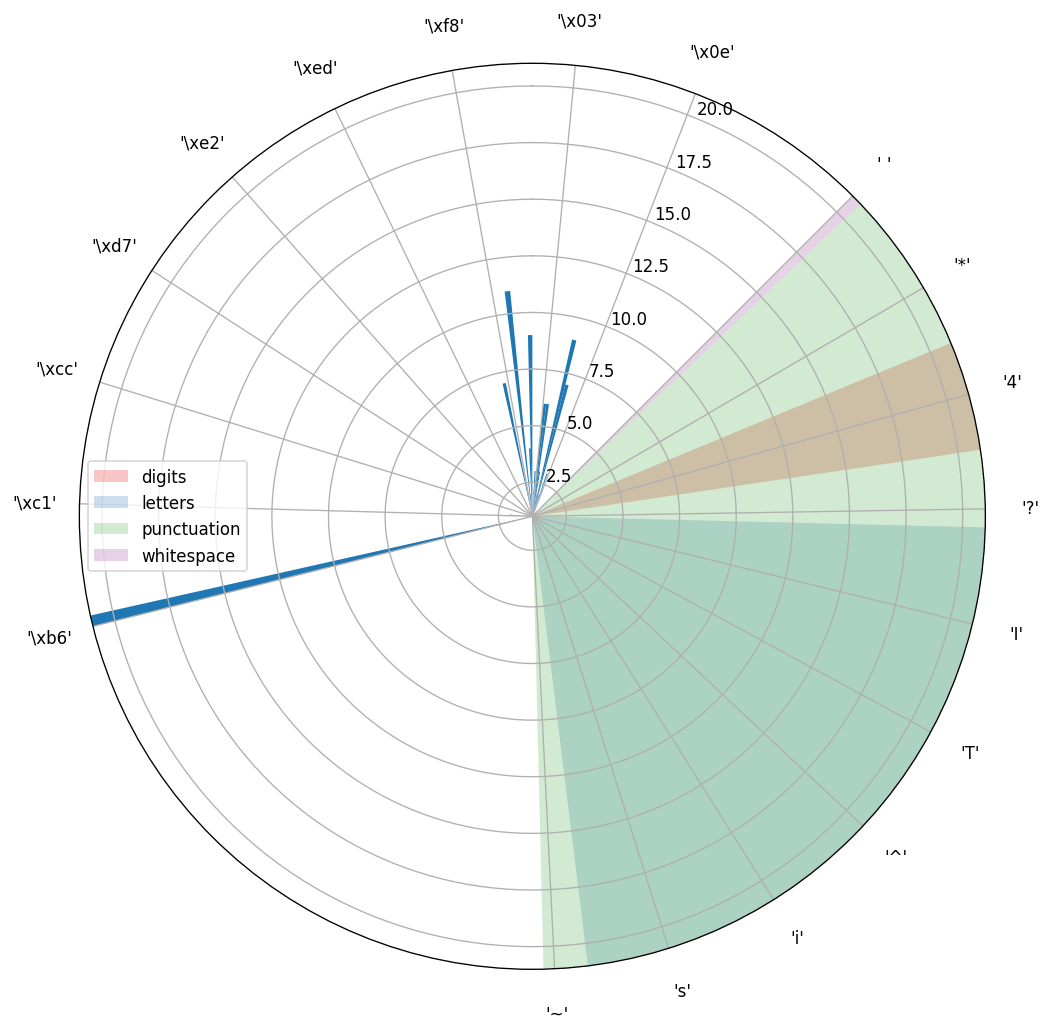
This graph looks very familiar, doesn’t it? It looks as if there was some offset N applied to the previous figure, whilst printable character area was left at the same place. And this is actually what happens with a text encrypted using Caesar cipher.

If you go clockwise, starting at a first non zero bar, until the last bar on the circle, you can say that it starts at 182 (‘\xb6’) and ends at 271 (‘\x0f’). Note that it has the same distance as in original text.

Breaking cipher

At this point it’s obvious that character, that is marked as '\xb6' on the later graph, corresponds to encrypted space. Which means that it should be enough to apply 106 ((106 + 182) % 256 == 32) shift to all characters to get the original text.

Let’s now have a look at the original challenge distribution:

OK, it looks slightly different from that picture we saw before, but it still looks similar to what we had. There’s a character '\' at the beginning (if you go clockwise), that stays away from others - this is likely to be an encrypted space. Having that, the only thing we need to do is to shift all characters on 196 (or 60 anticlockwise):

''.join(chr((ord(i) + 196) % 256) for i in ct)

This gives you:

Hey! Seems like you solved our challenge! We need people like you! Please send your solution and CV to icanbreakciphers@acme.com quoting reference: oIEhbmIyZWFeY2liwMDycw.

Congrats!

Wait, what? Are you saying that frequency distribution chart doesn’t look like in the example?

Breaking cipher with more than 1 shift

Do you see something like this?

I’m afraid, there’s no straightforward way to break this cipher unless it’s known that it was encrypted using Caesar cipher with multiple shifts. And by multiple shifts I mean that a shift depends on the position of elements in the text.

Let’s assume it’s a known fact that this text was encrypted using the following method using 6 different constants:

Let’s break down text on several strings by shift, that was applied to characters, which compose the string:

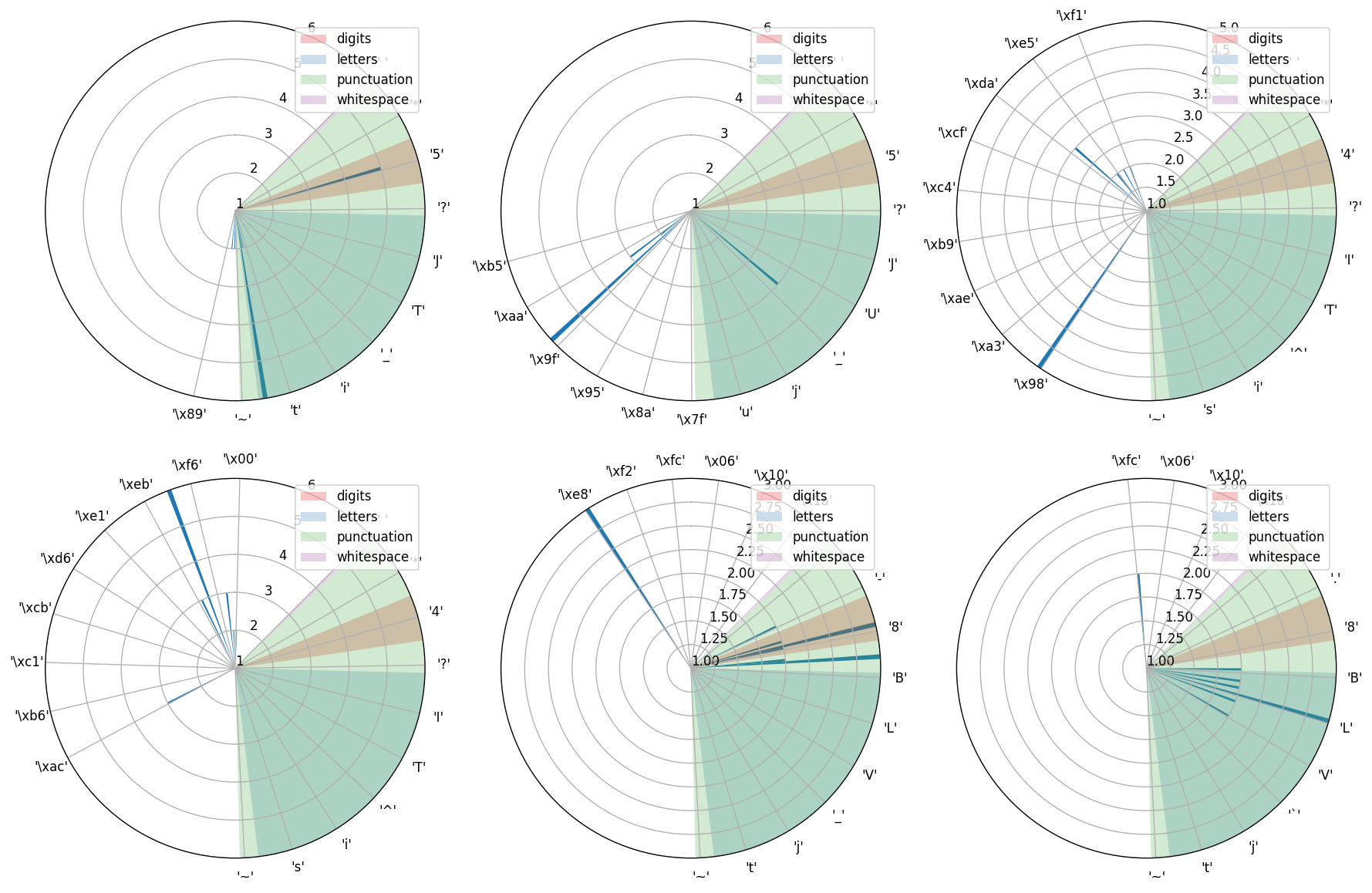
Oh, cool, if you look closely into those graphs you can spot bars, which stand out from other concentration of bars on a chart. I’m going to assume that those are encrypted spaces.

That doesn’t give us too much, does it? I don’t think so. At this point, I’d recommend to use the old good brute force.

Brute force without optimisation

Let’s do some math here. How long does it take to try all possible combinations in the worst case?

Providing that there are 6 different shifts, this gives us 2 ^ 48 possible combinations. Execution time of the following example function, that checks if there’s any meaningful English word in a sentence for a given possible cipher key, takes about 130µs on my machine (tested with timeit).

I know this is not a masterpiece and it can be optimised. en_dict here is a dictionary object from enchant package. That gives us (2 ^ 48) * 130 µs, which is approximately 423515 days. Speed of the function is not a real issue here, even if the function was blazingly fast and took 1µs per invocation, it would still take 3257 days in the worst case.

Hence we need to narrow down the number of guesses. Note that if a text was encrypted using only 3 shifts, you would need approximately 36 min even with this toy example to crack cipher. Using something faster than python, leveraging concurrency (go?, erlang?), cipher can be broken during a coffee break.

Brute force optimisation

There’s no point in trying all 0xff possible values. As long as our assumption is correct, we can try only those numbers, which, after applying to the text, would give us printable chars sequence. We can go even further and assume, that the source text is built from letters (uppercase and lowercase), digits, punctuation and that all the words are separated using space. If we find those codes at ASCII table, we can see that this sequence starts at 32 and ends at 126 '~', the span being 94 chars. This lowers the guess time to 1037 days.

Still bad, right? If we have a closer look at the encrypted text breakdown, we will see that all charts have their own span. For instance, first group starts at 52 ('4') and ends at 137 ('\x89'). We can only try to shift the encrypted text so far, so that upper bound does not exceed upper bound of printable ASCII characters, from which we assumed the source text was created. Hence in the best case 1st group of the text can be shifted by 236 to match 32 (' ') and in the worst case the last character has to be shifted by 245 to get 126 ('~'). This gives us range of 10 numbers, which are applicable for the 1st group. Applying the same logic to all group, it’s easy to see that the total number of guesses we have is 44.

From 2 ^ 48 down to 44, not bad, huh? There’s no point in further optimisation here. All 44 options can be guessed within a second.

PS: One might ask: this is not a complicated task, there’s no rocket science here… why did you write it? And my answer is - I just wanted to play with jupyter, matplotlib and write something here, in the blog! :) You can find notebook here: link to gist